Paleonapäťová analýza

Úlohou paleonapäťovej analýzy je stanovenie smerov a veľkostí štruktúrnotvorných napätí podľa charakteru deformačných štruktúr. Práca je zameraná na rekonštrukciu paleonapäťových polí z nameraných zlomov (tektonických zrkadiel mezoskopických rozmerov). Základným predpokladom je: poznať smer napätí, potom možno predvídať orientáciu a kinematiku vzniknutých zlomov (priama úloha); a naopak, ak je známa orientácia a zmysel pohybu na zlomoch, potom možno zrekonštruovať smer napätí, ktoré spôsobili ich vznik (inverse problem- obrátená úloha).

Rekonštrukcia paleonapätí podľa syngenetickej populácie novotvorených zlomov

Zlomy bežne vznikajú v systémoch s určitou symetriou. Takúto skupinu zlomov môžeme na základe geometrie definovať, ak vezmeme do úvahy vzťah k smeru sklonu a úklonu zlomových plôch, ako aj orientáciu a úklon striácií. Napríklad, ak majú zlomy rovnakú charakteristiku zlomovej plochy, ale odlišnú orientáciu striácií, nepatria k rovnakej skupine z hľadiska zlomového pohybu a orientácie napätí. Systém zlomov je tvorený dvoma a viacerými skupinami, ktoré spadajú pod rovnaký tektonický režim, takže ich mechanizmy sú konzistentné. Ide o homogénnu monogenetickú populáciu. Tiež platí, že ak súbor zlomov, ktoré pozorujeme v teréne tvorí geometrické zoskupenie, môže zahŕňať niekoľko systémov, ktoré sú výsledkom niekoľkých tektonických udalostí. V tomto prípade hovoríme o heterogénnej polygenetickej populácii. Párové zlomy jedného systému sú formované v tom istom čase pri pôsobení toho istého napäťového poľa a označujeme ich ako zlomy novotvorené. Vzťah medzi zlomami a napätiami, ktoré spôsobujú ich vznik bol teoreticky odvodený britským geológom Andersonom (1951) ako Andersonova zlomová teória. Vychádza z predpokladu, že povrch Zeme je „voľný“ a nepôsobí na neho strižné napätie. Na tento povrch však pôsobia tri na seba vždy kolmé normálové napätia σ₁, σ₂, σ₃. Jedno z týchto napätí je orientované kolmo na ňu (vychádzajúc z pôsobenia gravitácie, litostatického tlaku), pričom ostatné dve sú s ňou paralelné. Podľa Coulombovho frakturačného kritéria, strižné fraktúry obsahujú intermediálnu zložku napätia σ₂, a uhol medzi strižnou fraktúrou a maximálnym napätím σ₁ musí byť menší ako 45°. Typ zlomu, ktorý vzniká pri tejto situácii závisí na tom, ktoré z troch hlavných napätí je vertikálne. Na základe daných skutočností zostrojil svoj základný model čistého strihu pre vznik syngenetických zlomových porúch. Pričom jednotlivé typy zlomov (strižných porúch) odvodil rotáciou napäťového tenzora tak, aby každá z napäťových osí bola raz vertikálna. Týmto zostrojil prvú genetickú klasifikáciu zlomov, kde strižné poruchy rozdelil do poklesových, násunových a smerne-posuvných zlomov (obr. 1).

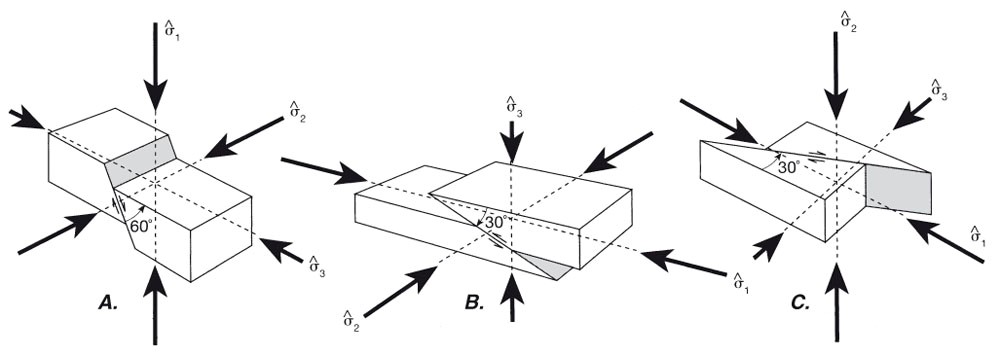
Obr. 1: ANDERSONOVA zlomová teória (upravené podľa Twiss & Moores, 2007)

Ak maximálne kompresné napätie σ₁ je vertikálne a pretína ostrý uhol medzi zlomovými plochami, zlomy ktoré takto vznikajú sú poklesy so sklonom 60°, kde nadložný blok poklesáva v smere strihu. Os σ₂ je v tomto prípade paralelná s prienikom medzi zlomovými plochami a os σ₃ je horizontálna a pretína tupý uhol medzi nimi. Ak je vertikálne minimálne kompresné napätie σ₃, vznikajú násuny s úklonom 30°, pričom nadložný blok sa pohybuje smerom hore. V prípade, že je vertikálna os σ₂, vznikajú vertikálne smerne-posuvné zlomy s horizontálnym smerom strihu. Rozdiel medzi párovými systémami poklesových a smerne-posuvných zlomov je len v ich orientácii. Ich orientácia je jednoducho vysvetlená 90° rotáciou okolo osi σ₃, pričom σ₂ si vymení pozíciu so σ₁. Systém párových prešmykových zlomov je interpretovaný jednoduchou 90° rotáciou okolo osi σ₁ párových smerne-posuvných zlomov. Vzájomný vzťah medzi napäťovým poľom a strižnými poruchami je východiskom pre  rekonštrukcie paleonapätí podľa syngenetickej populácie novotvorených párových zlomov (obr. 2). Ak je známy smer napätí, možno podľa definovanej geometrie predvídať orientáciu a kinematiku novovzniknutých zlomov. Ak má byť identifikovaný párový zlomový systém musia byť splnené nasledovné požiadavky: (a) prítomné sú dve skupiny zlomov; (b) striácie sú kolmé na smer prieniku zlomov; (c) zlomové sklzy musia mať opačný zmysel na protiľahlých zlomoch; (d) skracovanie je lokalizované v ostrom uhle a naťahovanie je lokalizované v tupom uhle medzi zlomovými plochami; (e) uhol medzi zlomami musí byť v súlade s mechanickými vlastnosťami hornín v čase vývoja párových zlomov.

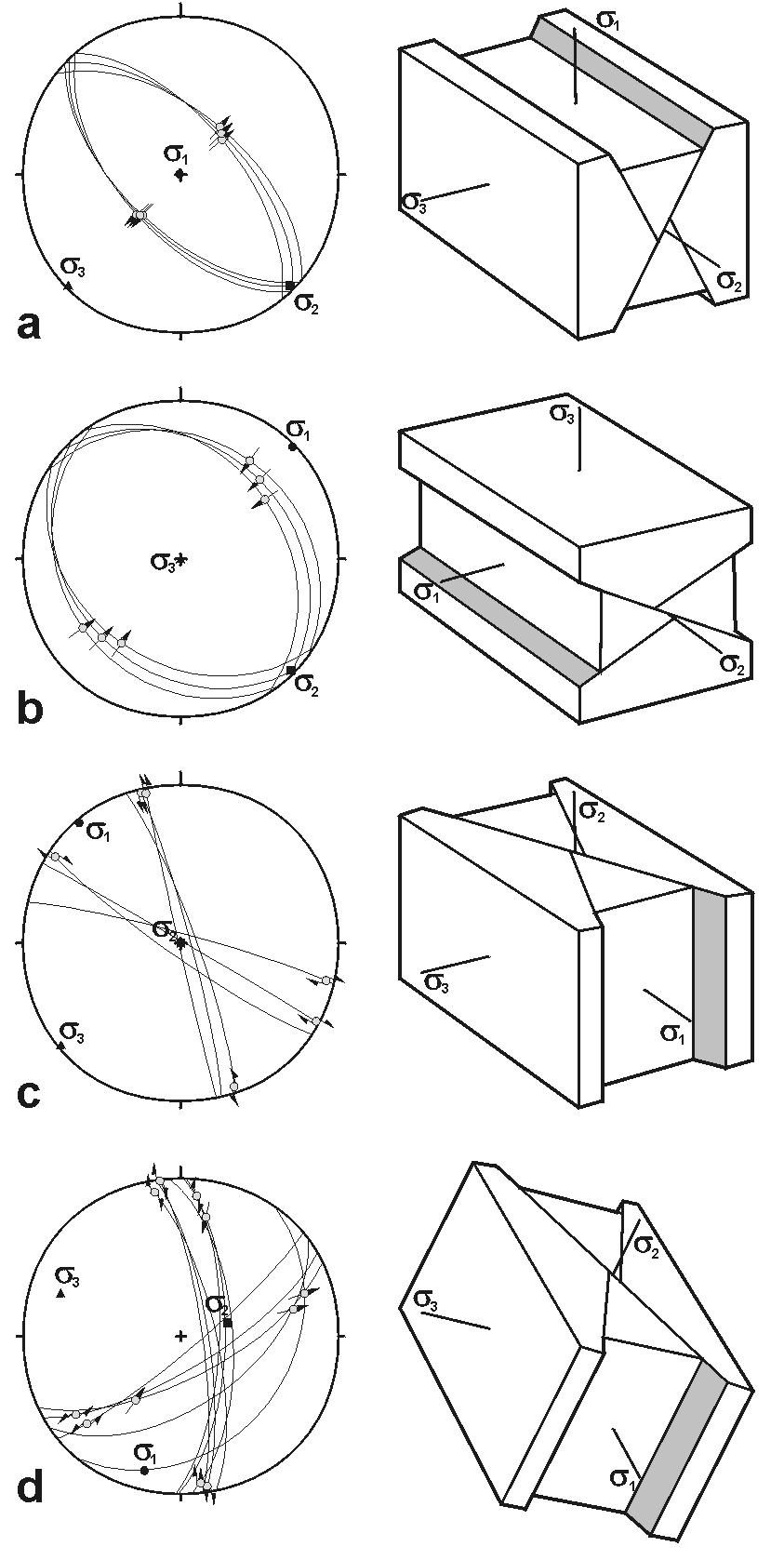
Obr. 2: Párové zlomové systémy a ich príklady zobrazené na stereogramoch (Angelier 1994)

Za predpokladu, že tieto podmienky budú splnené, potom paleonapäťové osi môžu byť rekonštruované ako je uvedené nižšie, pričom platí σ₁≥σ₂≥σ₃:

• napäťová os σ₁ pretína ostrý uhol medzi zlomami;
• napäťová os σ₂ zodpovedá prieniku dvoch zlomov;
• napäťová os σ₃ pretína tupý uhol medzi zlomami.

Identifikácia párových zlomových systémov je často zložitý problém. Pri určovaní hlavných napäťových osí by sa malo počítať aj s určitými nepresnosťami, ktoré sú výsledkom chybných meraní ako aj s rôznymi prírodnými nepravidelnosťami, preto by sa mali realizovať pomocou priemernej orientácie s odchýlkou maximálne do 15°. Keďže jednoduché tektonické napätie je zodpovedné za tvorbu zlomov, môže byť analýza párových zlomových systémov vykonávaná jednoduchými geometrickými prostriedkami. Ak sú v horninách prítomné predisponované plochy rôznych orientácií, ich aktivácia vo forme zlomov je častá. Vývoj originálneho párového systému môže byť v ojedinelých prípadoch až úplne potlačený. V takýchto prípadoch je mechanická analýza zložitejšia. Párové zlomy teda patria do špecifickej skupiny zlomov nazývaných novotvorené zlomy, ktoré vznikajú v jednom napäťovom režime (obr. 3, 4).

       

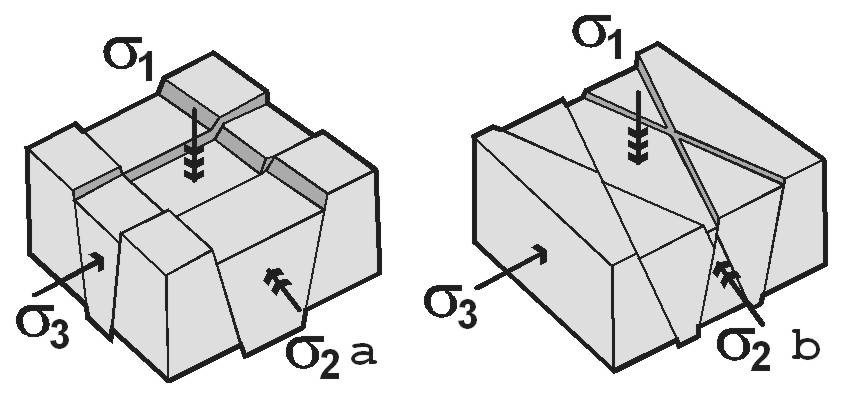
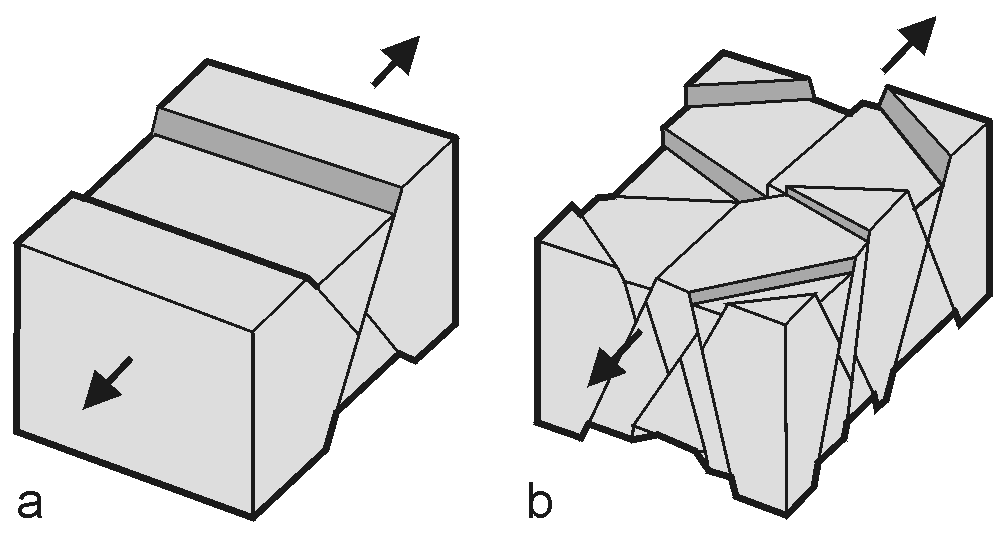
Obr. 3: Vznik párového systému zlomov (Angelier, 1994)

Rekonštrukcia paleonapätí podľa polygenetickej populácie reaktivizovaných zlomov

Pri pôsobení tektonického napätia sa môžu okrem vytvorenia syngenetickej populácie novotvorených zlomov reaktivovať aj preexistujúce poruchy, vzniknuté pri predchádzajúcich napäťových udalostiach. Ide o aktivizáciu tzv. zón oslabenia, ktoré existovali v horninách ešte pred pôsobením akéhokoľvek napätia. Preto je potrebné preskúmať aktiváciu predisponovaných plôch a reaktiváciu zdedených zlomových plôch. Tie môžu mať akúkoľvek orientáciu a v prípade, že sú vhodne orientované voči napätiam, zlomový sklz sa realizuje oveľa jednoduchšie. Väčšina už existujúcich plôch nespojitosti bola reaktivovaná vo forme zlomov počas nejakej tektonickej udalosti. Plochy oslabenia sa bežne vyskytujú dokonca aj v horninách, ktoré ešte neboli postihnuté krehkou deformáciou. Typickým príkladom sú pukliny chladnutia v plutónoch, pukliny spojené s vrstvovitosťou a diagenetické pukliny. Ich medzivrstvové špáry sú horizontálne, a takmer kolmé na niektorú hlavnú os napätia. Ak tam dôjde k nakloneniu plôch vrstvovitosti, môžu sa stať plochami odlepenia – décollementmi príkrovov, alebo sa z nich vyvíjajú poklesové a prešmykové zlomy. V prípade diagenetických puklín a puklín chladnutia je vysoko pravdepodobná ich aktivácia vo forme zlomov, pretože tieto pukliny sú rôzne orientované, čím sa zvyšuje pravdepodobnosť, že niektorý puklinový systém bude vhodne orientovaný voči hlavným paleonapäťovým osiam. Populácia takýchto porúch má polygenetický charakter.

Novotvorené zlomy vznikajú, keď krehká deformácia postihuje horniny, ktoré predtým neboli deformované. Naproti tomu, mladšie zlomové štruktúry sú zvyčajne komplikovanejšie. Pôvodný tektonický záznam je prepísaný, čoho výsledkom je zvyšovanie zložitosti štruktúr. Zlomy, ktoré vznikli v geologickej minulosti pri odlišných smeroch napätia nebývajú voči novému napäťovému poľu, ktoré spôsobilo ich reaktiváciu ideálne orientované ako párové zlomy. Pre takéto rôzne orientované reaktivované zlomy neplatí klasická andersonovská zlomová teória, ale je nutné použiť špeciálne metódy zohľadňujúce rejuvenizáciu pohybov na zlomoch.

Na výpočet orientácie napäťových osí na takýchto zlomoch je nevyhnutné definovať vzťah medzi smermi sklzov, čiže premiestnením na zlomovej ploche a napätiami, ktoré ich vyvolali. Pre interpretáciu základného vzťahu medzi distribúciou napätí na ploche oslabenia musíme vychádzať z mechaniky pevných látok, kde je napäťový vektor σ, ktorý pôsobí na ploche oslabenia F, teda na ploche poruchy. Napäťový vektor σ je rozložený na dva navzájom kolmé komponenty: normálové napätie ν, ktoré je kolmé na plochu F a strižné napätie τ, ktoré je paralelné s plochou F a je orientované v smere pohybu na poruche, pričom platí σ = ν + τ. Orientácia σ závisí na hlavných napätiach σ₁, σ₂, σ₃ a na polohe plochy F, ktorá je opísaná pomocou vektora n, kolmého na danú plochu.

Význam má aj normálové napätie ν, ktoré môže spôsobovať buď otváranie alebo zatváranie oslabených plôch. Ak je toto napätie totožné s napäťovým vektorom σ, môžu sa tvoriť tenzné trhliny (žily, dajky) alebo stylolity. K vzniku zlomu dochádza na ploche v prípade, že výrazne prevláda strižné napätie τ. Pohyb by mal byť paralelný s plochou F a zároveň by mal byť smer premiestnenia totožný s orientáciou maximálneho strižného napätia τ. Základom týchto metód je vzťah medzi napätím a sklzom na zlomových plochách. Táto hypotéza sa označuje ako Wallace-Bottova hypotéza. Stala sa východiskom ďalších štúdií, ktoré interpretovali napätia na zdedených zlomoch a je základom pre určenie napäťového tenzora zo zistených smerov a zmyslov pohybov na množstve zlomov s rôznou orientáciou, teda základom tzv. inverzného problému. Inverzná metóda spočíva v hľadaní takej orientácie a tvaru napäťového elipsoidu, ktorý by sa čo najviac približoval smerom strižných pohybov na analyzovaných poruchách. To znamená, že pomocou tejto metódy môžeme vypočítať tenzor napätí, pôsobením ktorého mohli vzniknúť pohyby na tektonických zrkadlách. Inverzná metóda predpokladá, že každá planárna plocha môže byť aktivovaná vo forme zlomu bez ohľadu na to, či ide existujúce zlomy (reaktivované zlomy) alebo o novotvorené zlomy, ktoré sa vyvinuli v danom napäťovom režime. Dôležité je určenie napäťového tenzora T, ktorý sa vzťahuje k orientácii a zmyslu sklzu na zlomovej ploche. Každé premiestnenie na zlomovej ploche je charakterizované smerom a zmyslom strižného napätia. To korešponduje s jednoduchým napäťovým tenzorom, ktorý je charakterizovaný troma napäťovými osami σ1, σ2, σ3.

Pri terénom meraní zväčša nameriame heterogénnu (polygenetickú) populáciu zlomov a určenie napäťového poľa nie je možné, keďže daná skupina, vznikala pri rôznorodej orientácii napätí. Je potrebné ju separovať na homogénne skupiny zlomov, ktoré vznikali pri jednom napäťovom tenzore. Podmienkou však zostáva, že všetky zlomy, ktoré sa pohli počas tej istej tektonickej udalosti a pohybovali sa nezávisle, boli pod vplyvom jedného napäťového tenzora. Ideálna zhoda pohybov vypočítaného napäťového tenzora na analyzovaných tektonických zrkadlách a skutočných pohybov nameraných podľa smerov striácií je zriedkavá. Dôvodom sú nepresnosti merania orientácie analyzovaných štruktúr alebo lokálne nepravidelnosti. Princíp tejto metódy preto spočíva v hľadaní najlepšej zhody medzi pozorovanými strižnými pohybmi na tektonických zrkadlách a orientáciou a tvarom vypočítaného napäťového tenzora, ktorý tieto pohyby mohol spôsobiť.

 

 

Hlavné napäťové osi: definícia, vzájomné vzťahy, napäťový elipsoid

Smer strižného pohybu (striácie) na zlome závisí nielen od smeru hlavných napäťových osí: σ₁ (maximálna kompresia),σ₂ (intermediárna kompresia),σ₃ (minimálna kompresia), ale aj od ich relatívnej veľkosti, teda od tvaru napäťového elipsoidu (obr. 4). Jeho tvar je určený pomerom veľkostí týchto osí a charakterizuje napäťové pole. Existuje veľké množstvo tvarov napäťového elipsoidu. Všetky varianty sa však nachádzajú medzi dvoma krajnými jednoosými elipsoidmi, ktoré majú rovnaké magnitúdy osi σ₂ a σ₃ alebo σ₁ a σ₂. Ide o jednoosú kompresiu, kde σ₁ je výrazne väčšia ako ostatné osi a jednoosú tenziu, kde v smere σ₃ je výrazná tenzia a σ₁, σ₂ sú minoritné a rovnaké. Dokázalo sa, že rovnako orientovaný zlom pri jednoosej tenzii a jednoosej kompresii má odlišný smer strihu, čiže na zlome sa generuje pohyb odlišného smeru, aj keď smer hlavných osí napätí  σ₁, σ₂, σ₃ pri oboch napäťových stavoch zostáva nezmenený. Tvar napäťového elipsoidu, ktorý je definovaný relatívnym pomerom veľkostí hlavných napäťových osí vyjadril ANGELIER (1975) pomocou parametra Φ ako: Φ=(σ₂-σ₃)/(σ₁-σ₃). Rozdielna definícia pomeru medzi hlavnými napäťovými rozdielmi používa symbol R, kde R=(σz-σx)/(σy-σx). Rozdiel medzi Φ a R leží v rozsahu ich možných hodnôt. R nadobúda hodnoty z intervalu <-∞ až +∞>, lebo hlavné napäťové magnitúda σx, σy, σz sú uvádzané bez predpokladu o ich poradí. Parameter Φ nadobúda hodnoty od 0–1, pretože je jasne definovaný vzťah medzi paleonapäťovými osami, kde σ₁≥σ₂≥σ₃. Pričom hodnota Φ=0 zodpovedá jednoosej kompresii a hodnota Φ=1 zodpovedá napäťovému stavu jednoosej tenzie. Parameter sa nemení po znásobení, resp. zmenšení magnitúd hlavných osí napätia, mení sa len poloha elipsoidu vyjadreného Mohrovými kružnicami po horizontálnej osi v Mohrovom diagrame.

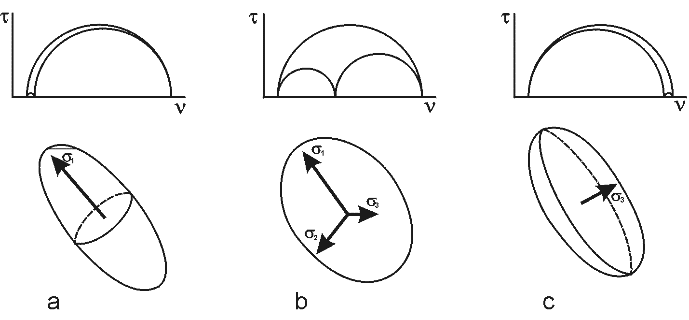
Obr. 4: Napäťové elipsoidy: a) protálny jednoosý kompresný elipsoid, b) trojosý elipsoid, c)oblátny jednoosý extenzný elipsoid (ANGELIER, 1994).

 

Výpočet redukovaného a kompletného napäťového tenzora

Redukovaný napäťový tenzor môžeme vypočítať z polygenetickej populácie zlomov, ktoré boli reaktivované pri určitom napätí. Definujú ho štyri premenné: smer hlavných osí napätia σ₁, σ₂, σ₃ a parameter Φ. Keďže pri výpočte redukovaného tenzora sa rieši rovnica o 4 neznámych, sú potrebné najmenej 4 zlomy. Toto je limitujúci prvok pre inverznú metódu. Keďže smer strihu na náhodne orientovanom zrkadle závisí aj od tvaru napäťového elipsoidu (Φ), jedno tektonické zrkadlo umožní vymedziť len rozpätie možných smerov osí napäťových elipsoidov, ktoré by pohyb na danom zrkadle mohli spôsobiť. Preto nie je možné z jedného zlomu vypočítať presný smer osí. Pri výpočte sa hľadá taký napäťový elipsoid, ktorý by najlepšie vyhovoval pozorovaným pohybom na tektonických zrkadlách svojim tvarom a orientáciou. Presnosť výpočtu tenzora pre danú populáciu porúch je definovaná kritériom F_1.  Ide o uhol medzi pozorovaným smerom ryhovania a teoretickým strihom, ktorý by na zrkadle vznikol pôsobením vypočítaného tenzora. Vo všeobecnosti platí, že čím je uhol menší, tým je výsledok presnejší. V praxi sú akceptovateľné uhly F₁<20°. Vyššia hodnota F₁  svedčí o tom, že na výpočet tenzora bola použitá polyfázová populácia porúch. Preto je potrebné odseparovať rôzne generácie a napäťový tenzor počítať len z monofázových populácií. Hodnota uhla F₁ sa najčastejšie používa ako diskriminačné kritérium pri inverznej metóde.

Na výpočet kompletného napäťového tenzora je potrebné poznať absolútne veľkosti (magnitúda) hlavných napätí σ₁, σ₂, σ_3. Nimi je definovaná jeho pozícia v Mohrovom diagrame (definuje vzťah medzi strižným (τ) a normálovým (ν) napätím), ktorá závisí od súčiniteľov k a l. Hodnotami k a l sa násobia relatívne jednotkové veľkosti osí napätí, ktoré sú dané parametrom Φ. Súčiniteľ k je pozitívna konštanta, ktorá mení veľkosť Mohrovho diagramu bez zmeny parametru Φ. Súčiniteľ l je prírastok alebo úbytok izotrópnej zložky napätia. Je pozitívny pre kompresiu a negatívny pre extenziu a na základe toho posúva napäťový tenzor do kompresnej alebo tenznej časti Mohrovho diagramu po horizontálnej osi. (obr. 5).

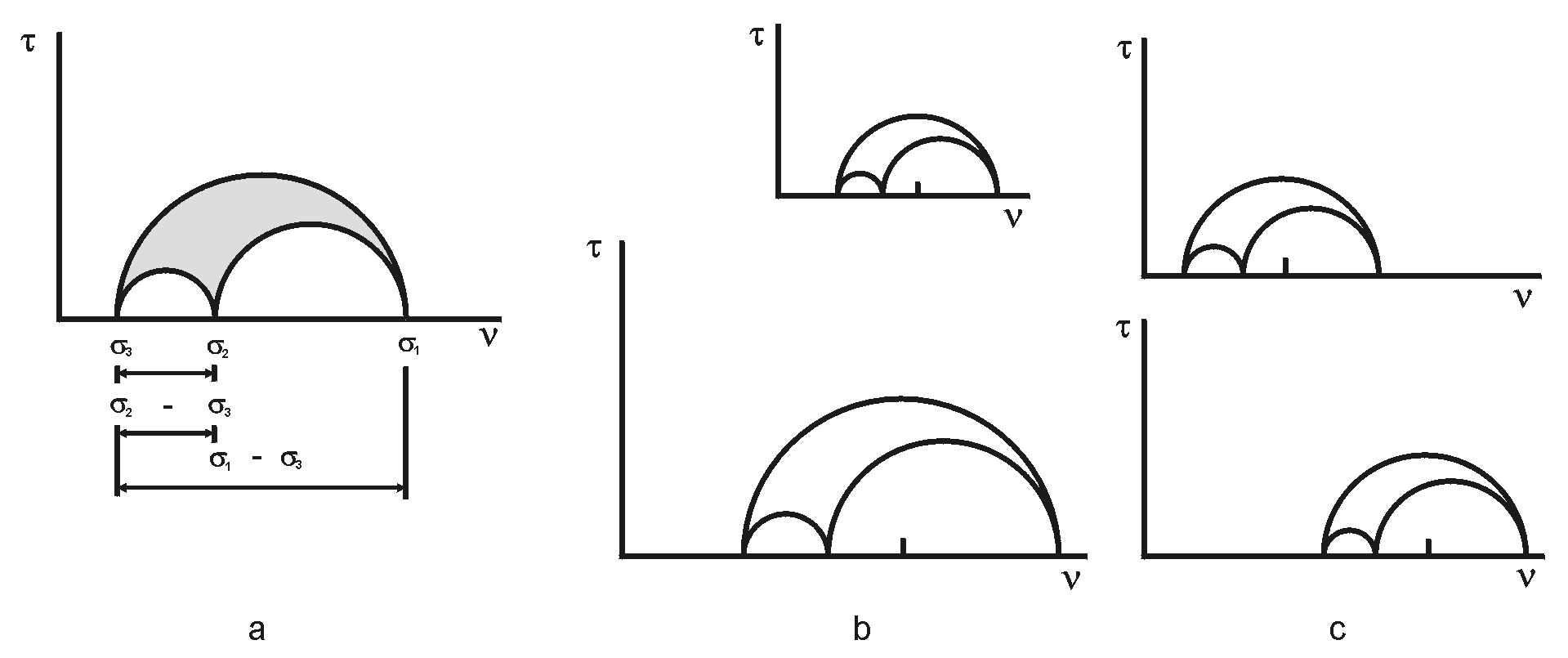
Obr. 5: Mohrove diagramy (upravené podľa Angelier, 1994)

Pri výpočte týchto súčiniteľov sa vychádza z troch kritérií (obr. 6):

• kritérium vzniku párových zlomov – môžeme použiť v prípade, že v analyzovanej populácii zlomov boli zistené novotvorené párové zlomy. Magnitúda normálového a strižného napätia pre párové zlomy zodpovedajú bodu na veľkej polkružnici Mohrového diagramu a sú charakterizované dihedrálnym uhlom 2θ medzi týmito párovými zlomami. Obalová krivka, ktorá limituje podmienky vzniku párových zlomov sa dotýka Mohrovej kružnice v bode, ktorého spojnica so stredom zviera s horizontálnou osou diagramu uhol 2θ.
• kritérium uhla vnútorného trenia – uhol vnútorného trenia ω je uhol medzi priamkou, ktorá vychádza zo stredu diagramu a vodorovnou osou diagramu. Tento uhol vlastne charakterizuje veľkosť iniciálneho trenia. Všetky zdedené zlomy zodpovedajú predisponovaným horninovým diskontinuitám (vrstevnatosť, pukliny, staré zlomy, atď), ktoré sa pohli v zodpovedajúcom napätí. Výskyty sklzov na takýchto zlomových plochách sú kontrolované zákonom trenia, takže zodpovedajú bodom v Mohrovom diagrame. Teda ak sa pohli v danom napäťovom stave musia ležať nad priamkou trenia a samozrejme vnútri najväčšej kružnice, ktorá vymedzuje hodnoty extrémnych osí napäťového poľa.
• kritérium vertikálneho napätia – je založené na predpoklade, že  jedna z hlavných napäťových osí býva vertikálna. Os σ₁ je vertikálna v extenznom režime, pri tvorbe poklesov. Osi σ₂ a σ₃ sú vertikálne pri kompresných režimoch, pri ktorých sa tvoria smerné posuny a prešmyky. V prípade, že sa podarí vypočítať litostatický tlak v mieste vzniku poruchy, získa sa absolútna hodnota magnitúda vertikálne orientovaného napätia σ_v. Ak sa podľa kinematického charakteru na poruche určí tektonický režim, jednej z hlavných osí napäťového tenzora sa priradí hodnota σ_v. Na základe parametra Φ sa na Mohrovom diagrame dajú určiť veľkosti ostatných osí hlavných napätí.

 

Obr. 6: Kritéria na určenie magnitúd hlavných osí napätí (upravené podľa Angelier, 1994)

 

Tektonický režim

Tektonický režim, ktorý je definovaný napäťovým tenzorom, charakterizujú tri hlavné napäťové osi (σ1, σ2, σ3). Podstatou je nájdenie určitého napäťového tenzora, zo všetkých údajov zo zlomov, ktorý by vyhovoval všetkým zlomovým plochám. To pri nameraní heterogénnej populácie zlomov nie je možné. Dôležité je určiť všetky zlomy, ktoré sa nezávisle od seba pohli počas tej istej tektonickej udalosti a zároveň pod vplyvom rovnakého napäťového tenzora. Na základe orientácie napäťových osí a tvaru napäťového elipsoidu určíme hlavné napäťové režimy: extenzný, pri ktorom os σ1 je vertikálna; smerne posuvný, kde je vertikálna os σ2 a kompresný s vertikálnou osou σ3. Z týchto 3 typov môžeme určiť ďalšie kombinované napäťové režimy, ktoré závisia od parametra R. Hlavné typy napäťových stavov vyjadríme číselným indexom R´ s hodnotami od 0 po 3, ktorý je definovaný nasledovne:

 

R´=R, keď σ1 je vertikálna – extenzný režim

R´= 2-R, keď σ2 je vertikálna – smerne – posuvný režim

R´= 2+R, keď σ3 je vertikálna – kompresný režim